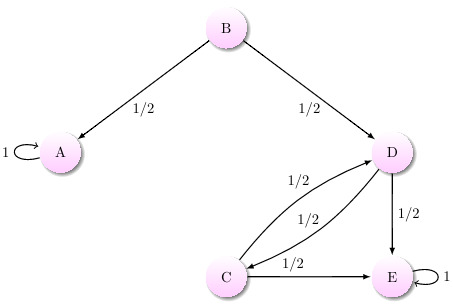

An absorbing Markov chain A common type of Markov chain with transient states is an absorbing one. An absorbing Markov chain is a Markov chain in which it is impossible to leave some states, and any state could (after some number of steps, with positive probability) reach such a state. It follows that all non-absorbing states in an absorbing Markov chain are transient.
An absorbing state is a state \(i\) in a Markov chain such that \(\mathbb(X_ = i \mid X_t = i) = 1\). Note that it is not sufficient for a Markov chain to contain an absorbing state (or even several!) in order for it to be an absorbing Markov chain. It must also have all other states eventually reach an absorbing state with probability \(1\).
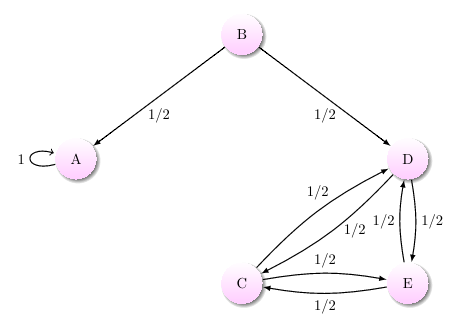
A Markov chain with an absorbing state that is not an absorbing Markov chain
If the chain has \(t\) transient states and \(s\) absorbing states, the transition matrix \(P\) for a time-homogeneous absorbing Markov chain may then be written as \[P = \begin Q & R \\ \text & I_s \end,\] where \(Q\) is a \(t \times t\) matrix, \(R\) is a \(t \times s\) matrix, \(\text\) is the \(s \times t\) zero matrix, and \(I_s\) is the \(s \times s\) identity matrix.

A simple example of an absorbing Markov chain is the drunkard's walk of length \(n + 2\). In the drunkard's walk, the drunkard is at one of \(n\) intersections between their house and the pub. The drunkard wants to go home, but if they ever reach the pub (or the house), they will stay there forever. However, at each intersection along the way, there is a probability \(p\), typically \(\frac\), that the drunkard will become confused and, losing their sense of direction, return to the previous intersection.
A drunkard's walk with \(n=3\) and \(p=\frac\)
Taking Pub to be the \(4^\text\) state and Home to be the \(5^\text\) state, the transition matrix is \[\begin 0 & \tfrac & 0 & \tfrac & 0 \\ \tfrac & 0 & \tfrac & 0 & 0 \\ 0 & \tfrac & 0 & 0 & \tfrac \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end.\] It follows that \[Q = \begin 0 & \tfrac & 0 \\ \tfrac & 0 & \tfrac \\ 0 & \tfrac & 0 \end \hspace \text \hspace R = \begin \tfrac & 0 \\ 0 & 0 \\ 0 & \tfrac \end.\]
Many calculations for Markov chains are made simple by that decomposition of the transition matrix. In particular, the fundamental matrix \(N = (I_t - Q)^\) contains a lot of information. Note \[N = (I_t - Q)^ = \sum_^\infty Q^k,\] so \[\begin N_ &= \text(X_0 = j \mid X_0 = i) + \text(X_1 = j \mid X_0 = i) + \text(X_2 = j \mid X_0 = i) + \dots \\ &= \mathbb(\text j \text < is visited>\mid X_0 = i). \end\]
It follows from the linearity of expectation that, starting from state \(i\), the expected number of steps before entering an absorbing state is given by the \(i^\text\) entry of the column vector \(N \, \mathbf\).
Furthermore, the probability of being absorbed by state \(j\) after starting in state \(i\) is given by the \((i,\,j)^\text\) entry of the \(t \times s\) matrix \(M = N\, R\), \[ M_ = \sum_^t \text(X_ = j \mid X_t = k) \mathbb(\text k \text < is visited>\mid X_0 = i).\]
What is the probability the drunkard, starting at intersection \(1\) or \(2\), makes it home in the above example?
Note \[N = (I - Q)^ = \begin 1 & -\tfrac & 0 \\ -\tfrac & 1 & -\tfrac \\ 0 & -\tfrac & 1 \end^ = \begin \tfrac & 1 & \tfrac \\ 1 & 2 & 1 \\ \tfrac & 1 & \tfrac \end.\] Then, \[M = \begin \tfrac & 1 & \tfrac \\ 1 & 2 & 1 \\ \tfrac & 1 & \tfrac \end \begin \tfrac & 0 \\ 0 & 0 \\ 0 & \tfrac \end = \begin \tfrac & \tfrac \\ \tfrac & \tfrac \\ \tfrac & \tfrac \end.\] So the drunkard has probability \(\tfrac\) of making it home from intersection \(1\) and probability \(\tfrac\) of making it home from intersection \(2\).